An introduction to Steven Lehar, part III: Flame fronts and shock scaffolds

In the previous two posts, we covered Lehar’s bubble world model of phenomenology and harmonic resonance model of neuroscience, respectively. This post is intended to serve as a crash course in visual reification, which I hope should bridge the two conceptually. Throughout, I have worked with the graphic artist Scry Visuals to create animated visualisations of some of Lehar’s original diagrams and figures.

This post also marks the point at which I must hand off from the Leharian paradigm to the non-linear wave computing paradigm developed by the team at the Qualia Research Institute – we’ll spend some time looking at how their work builds upon Lehar’s.

I would like to be able to lean upon a computational metaphor to illustrate how all this fits together. Perhaps if your brain were a computer, then harmonic resonance would describe the computer’s architecture, and the bubble world model would describe the computer’s screen? The metaphor crumbles, however, when we introduce visual reification. I would like to be able to say that visual reification is a program that the computer runs; but as we shall see, it is as if this program were to run on the screen itself. This is quite unlike any computer that I know of!

Over the centuries, the metaphors we have used to make sense of the brain have evolved to keep pace with our most complex technologies. The ancient Greeks were fond of pneumatic metaphors, and Freud himself liked his hydraulics. The Industrial Revolution gave rise to mechanical clockwork, steam engines, and telegraph lines; and as we arrived at the Information Age it appeared as though we could understand anything through the computer and the universal logic of the Turing machine.

But the brain is no more a digital computer than it is a truck or a series of tubes; and so lacking a good metaphor I must present Lehar’s model as a thing unto itself.

The Constructive Aspect of Visual Perception: A Gestalt Field Theory Principle of Visual Reification Suggests a Phase Conjugate Mirror Principle of Perceptual Computation

Many gestalt illusions reveal a constructive, or generative aspect of perceptual processing where the experience contains more explicit spatial information than the visual stimulus on which it is based. The experience of gestalt illusions often appears as volumetric spatial structures bounded by continuous colored surfaces embedded in a volumetric space.

These, and many other phenomena, suggest a field theory principle of visual representation and computation in the brain. That is, an essential aspect of neurocomputation involves extended spatial fields of energy interacting in lawful ways across the tissue of the brain, as a spatial computation taking place in a spatial medium. The explicitly spatial parallel nature of field theory computation offers a solution to the otherwise intractable inverse optics problem; that is, to reverse the optical projection to the retina, and reconstruct the three-dimensional configuration of objects and surfaces in the world that is most likely to have been the cause of the two-dimensional stimulus.

A two-dimensional reverse grassfire algorithm, and a three-dimensional reverse shock scaffold algorithm are presented as examples of parallel spatial algorithms that address the inverse optics problem by essentially constructing every possible spatial interpretation simultaneously in parallel, and then selecting from that infinite set, the subset of patterns that embody the greatest intrinsic symmetry. The principle of nonlinear wave phenomena and phase conjugate mirrors is invoked as a possible mechanism.

The Constructive Aspect of Visual Perception is listed on Lehar’s homepage as one of his principal papers. It describes a proposed field-based computational process by which the brain reifies, or stabilises a pair of two-dimensional retinal images, and then combines them into one two-dimensional image plus a depth map – sometimes colloquially referred to a two-point-five-dimensional image – also known as the worldsheet, as covered in part one.

This is a lot to unpack. Perhaps it is best to open with a definition of the word reify. Wiktionary lists its etymology as follows:

Formed from the Latin rēs (“thing”) + -ify (English suffix).

I would offer the definition: to turn mentally into a thing. In my mind it conjures imagery of construction, be it of a sandcastle on the beach or a brutalist concrete monolith.

Most commonly it is applied to ideas. Some people reify ideas with a particular zest – over the centuries much ink has been spilt and tears have been shed over who gets to reify what – while others remain conscientious objectors in the realm of thought-constructs.

At a less abstract, sensory level, the brain also reifies a sparse collection of raw sensory inputs into a crisp and stable world simulation. With regards to vision, the retinal image as it arrives in the visual cortex is grainy, noisy, rife with imperfections, and yet the brain performs the remarkable task of cleaning it up.

First of all, the early layers of the visual cortex subject incoming visual information to heavy pre-processing, primarily edge detection. The reader may recognise this process from the predictive processing model of neuroscience – sensory input is compared to predicted sensory input, and only the difference between the two is retained – which we call prediction errors.

Scott Alexander describes this process in his book review of Surfing Uncertainty:

The key insight: the brain is a multi-layer prediction machine. All neural processing consists of two streams: a bottom-up stream of sense data, and a top-down stream of predictions. These streams interface at each level of processing, comparing themselves to each other and adjusting themselves as necessary.

The bottom-up stream starts out as all that incomprehensible light and darkness and noise that we need to process. It gradually moves up all the cognitive layers that we already knew existed – the edge-detectors that resolve it into edges, the object-detectors that shape the edges into solid objects, et cetera.

At the lowest level of this stack, this is somewhat isomorphic to high-passing the incoming image stream. In the spatial domain, we retain the high-frequency information – the edges – while the low-frequency information – large flat areas – tend to get normalised out.

Lehar’s paper concerns what happens next. I would like to return to part two briefly, where we discussed how Lehar is working with a electromagnetic field theory of consciousness:

The leap of faith we may yet then take is that this field system also represents the structure of our experience via some unknown isomorphism – that our worldsim, our model of volumetric experience is embedded in there somehow. The field is not an epiphenomenon; it is the one and same as our subjective phenomenal experience, and it performs some useful computational role by virtue of its dynamics.

Whether or not one is agnostic to such theories – a well-developed example would be Susan Pockett’s Consciousness Is a Thing, Not a Process (2017) – what is relevant is that any field substrate would likely support wave dynamics of some nature. I understand that at the time of writing, such theories remain on the fringe. If the reader is skeptical, I would like to make but one argument: one thing we do know about evolution is that it’s a tremendous cheapskate. So, which do you think is cheaper: simulating wave phenomena using a neural network, or exploiting a substrate which already supports them?

What Lehar (and myself) would like to demonstrate is how wave phenomena could be harnessed to perform the useful computational role mentioned earlier – that of reifying visual objects. The spirit of this post is such that if this theory has predictive power and reflects our subjective experiences, then perhaps that should count in favour of a field-like consciousness substrate.

Flame fronts

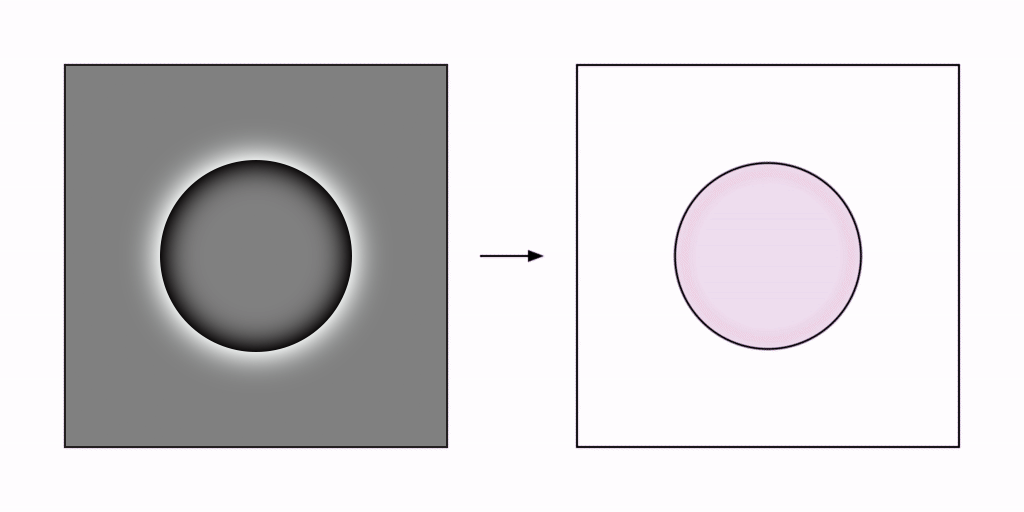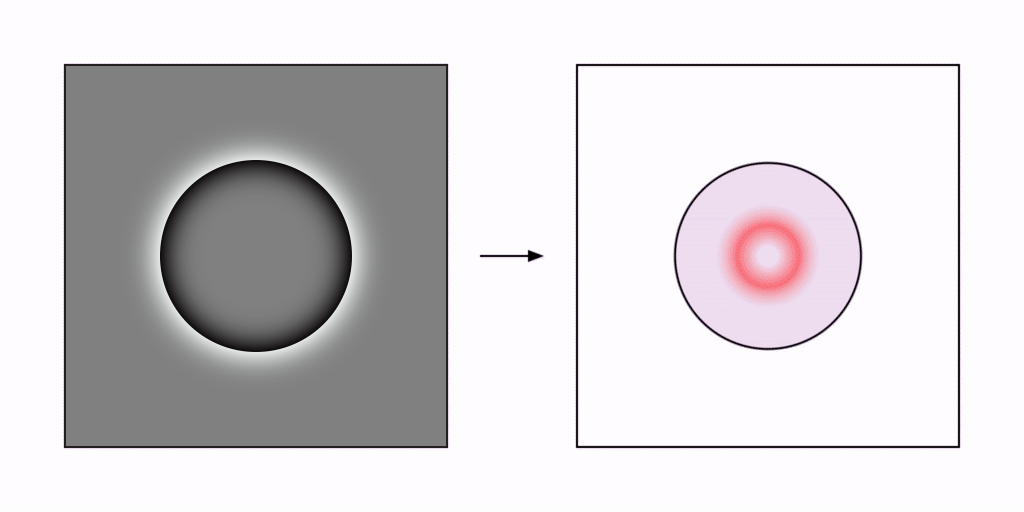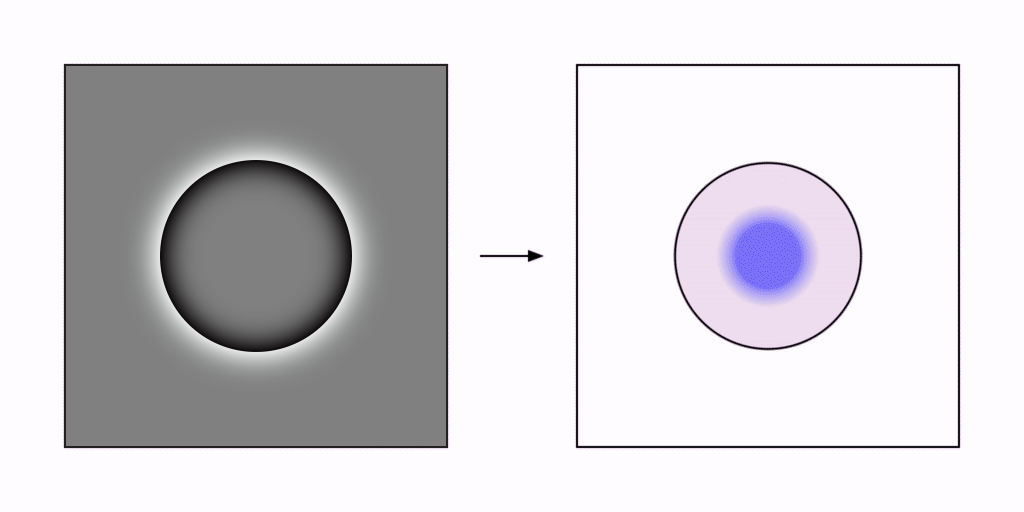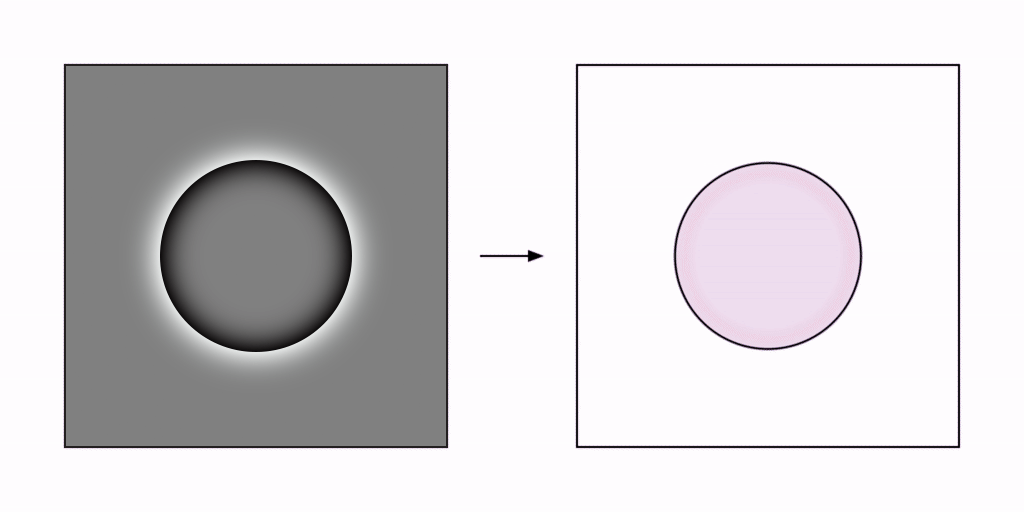
Let us start with an example of a black circle on a white background. After the initial high pass, we would be left with a black inner gradient inside a white outer gradient, suspended in a region of no stimuli at all.

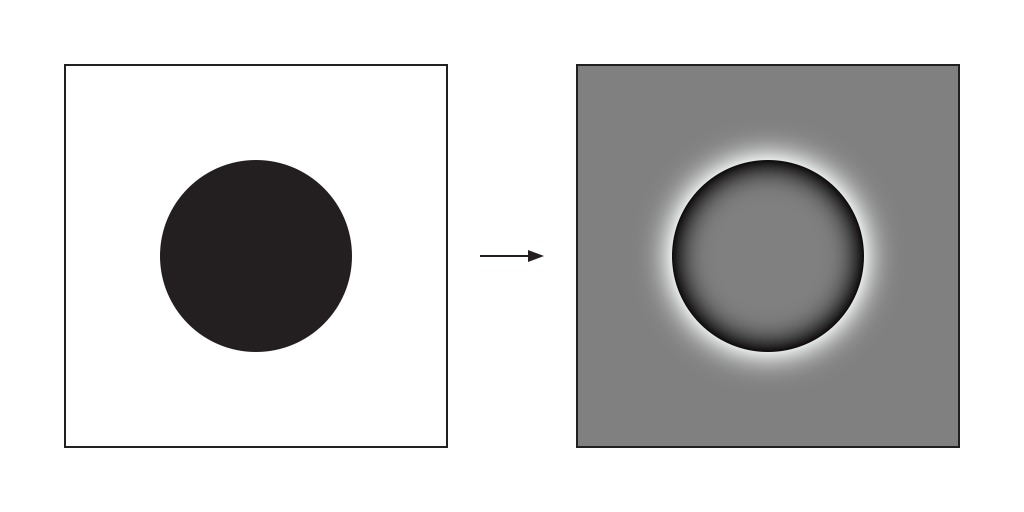
The image on the right is a representation of what might get injected into our phenomenal fields. As that happens, waves propagate outwards in all directions from the source of stimulation. Lehar uses the term flame front or grassfire to describe this process – as if a fire was lit at the edge of the stimulus and allowed to burn in all directions. In his words:

Soap bubbles, and water seeking its level, are spatial field-like processes, but they are not computational algorithms as such, until or unless they are deployed in some kind of computational mechanism. The grassfire metaphor on the other hand is a computational algorithm used in image processing that uses a field theory principle of computation to compute the medial axis skeleton of plane geometrical shapes, such as squares or circles or triangles. The idea is to ignite the perimeter of the geometrical pattern in question, and allow the flame front to propagate inward to the center of the figure like a grass fire.

The grassfire algorithm is a mathematical abstraction rather than a field-like physical phenomenon. It exploits the regular propagation or diffusion of some idealized signal through a uniform medium, as the mechanism that performs the actual computation. The algorithm can be implemented in a variety of different physical ways, from actual lines of fire burning across a field of dry grass, to chemical reactions like the Belousov-Zhabotinsky reaction involving reaction fronts that propagate uniformly through a chemical volume, to computer simulations of an idealized spatial signal propagating in an idealized medium.

In this situation, the white outer wavefront would shoot off into nothingness – as if you threw a rock into the ocean. But the black inner wavefront remains trapped by the continually reinforced perimeter – as if you shook the rim of an above-ground swimming pool.

As the black wavefront progresses towards the center of the circle, it rises in amplitude before rebounding off of itself as a reverse flame front, flood-filling the circle with black on the way back out again – and thus forms our circular standing wave, with a cyclical process of bottom-up perception and top-down reification.

I propose that the reification of features observed in perception is computed as a kind of pseudo-inverse processing of the bottom-up feed-forward processes by which those features were detected in the first place. The grassfire algorithm can be used to clarify this concept by adding a second, reverse-grassfire processing stage to perform the reification.

Hang on. Many years ago my mum and dad’s house had a circular above-ground swimming pool much like I described just now – and I know for a fact that it doesn’t fill itself up if you make waves in it – quite the contrary! What’s going on?

Nonlinear waves

The key concept is that of linearity. A linear system should be invariant in certain ways – if you scale or translate the inputs, the outputs should be scaled or translated correspondingly. The superposition principle states that in a linear system, when two waves meet, their amplitudes sum – you briefly have one wave that’s double the height – and then they separate once again, without losing or exchanging any energy.

In linear media, such as a deep wave pool, waves pass through one another in a transparent fashion as described. In certain nonlinear media, such as a shallow wave pool, waves can exchange energy with themselves or the medium: they can reflect off one another, or form standing waves in unusual ways. This said, I should note that in reality, mechanical concerns mean that no fluid wave system is likely to be truly linear; even in a deep wave pool you will still see some dispersion.

A case of a nonlinear system familiar to musicians may be that of a distortion pedal. By amplifying the input signal to the point where the electric circuit saturates, the output signal is clipped, gaining its characteristic harmonic overtones. In this case, the transfer function of the circuit could be considered nonlinear.

It’s an open question where the nonlinearities in this field system might come from. Lehar suggests that something called phase conjugation, observed in nonlinear optics, exhibits the required properties:

There is a very interesting phenomenon observed in nonlinear optics called phase conjugation, that just happens to mirror some of the reconstructive properties of perceptual reification. In fact, a nonlinear standing wave model exhibits many of the properties of a forward-and-reverse grassfire algorithm cycling repeatedly between abstraction and reification half-cycles. I propose that phase conjugation is the computational principle behind perceptual reification by symmetry completion.

Andrés Gómez Emilsson discusses nonlinear optics in much greater detail in his video, Nonlinear Wave Computing: Vibes, Gestalts, and Realms:

But nonlinearities also happen in other places, something that Steven Lehar made me aware of. It’s essentially nonlinear optics. If you combine two lasers in a quartz, or many other crystal materials, they will form an interference pattern where you’re over-energizing the precise interference pattern of the superposition of those two lasers. Something really weird happens – that intersection point will work as a retroreflector, meaning that if you shine another laser at it, it will reflect not like a mirror but like a retroreflector – like the kind of thing that you put on your bicycle or car. So however you shine the light, it bounces back to you.

So again, light is usually linear in its behavior but in some mediums it can become very nonlinear. The reason why that happens is that electric fields can change the refractive index of some materials. So the laser, if it gets strong enough, will induce an electric field which changes the refractive index, and as a consequence, it’s going to bend the light. You get these weird effects like self-focusing for example, where if you shine a laser at a certain energy regime the laser just goes through, no problem. You increase the energy and all of a sudden it’s out of focus and it focuses on just a point and may explode because it just is such a high temperature. So all of that is nonlinear optics and those are nonlinear waves.

We’ll come back to refraction later. If this is all a little bit much, suffice it to say that the nonlinearities of the wave medium are that which grant it the magical properties it requires in order to sustain these standing waves corresponding to stable percepts. These nonlinearities are also what permit this wave medium to perform irreversible computation, discarding redundant sensory information in exchange for a better fit world model.

Symmetry

Let’s move on. Your visual system is capable of rendering shapes other than circles. How about some ellipses?

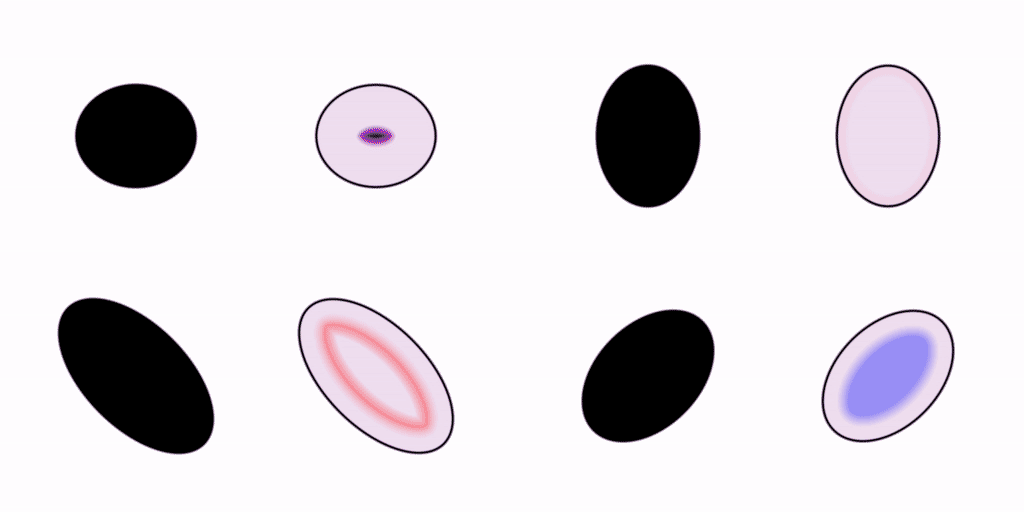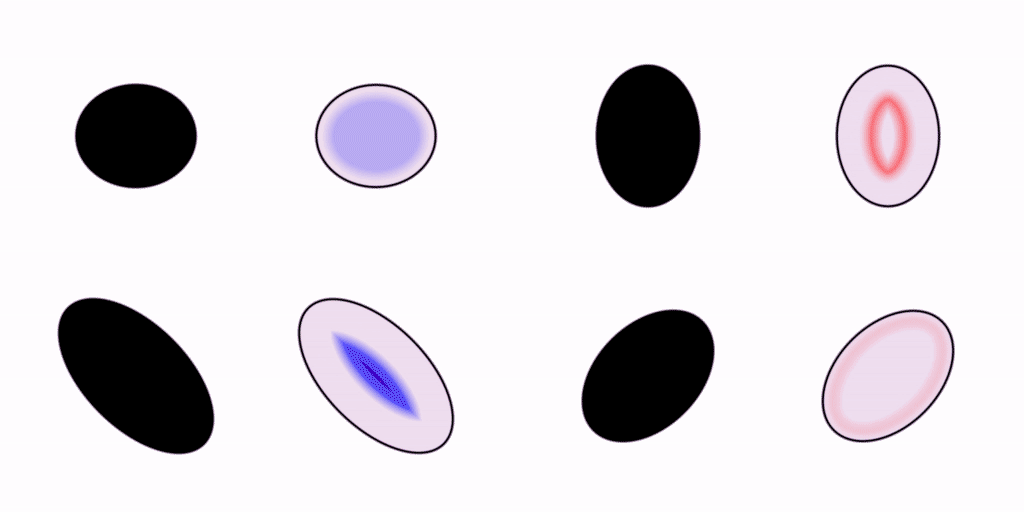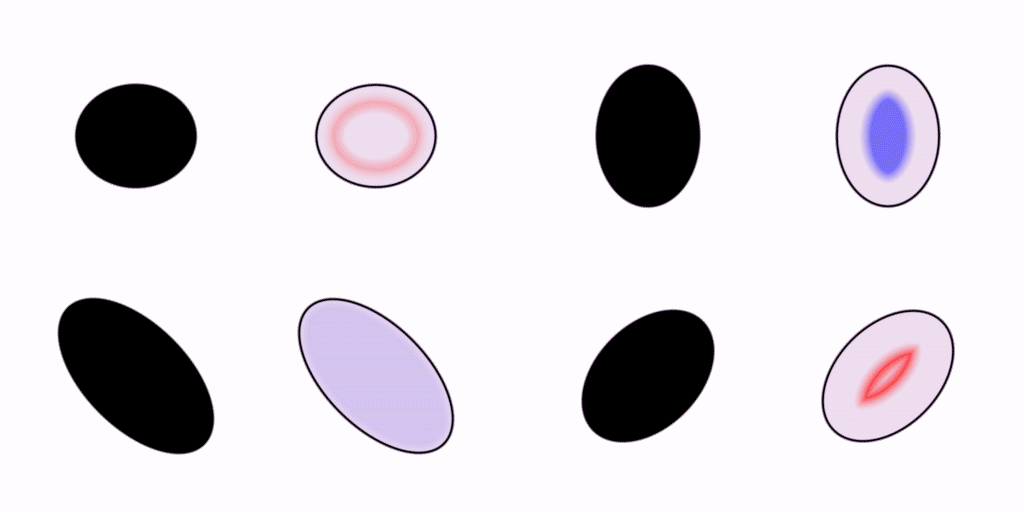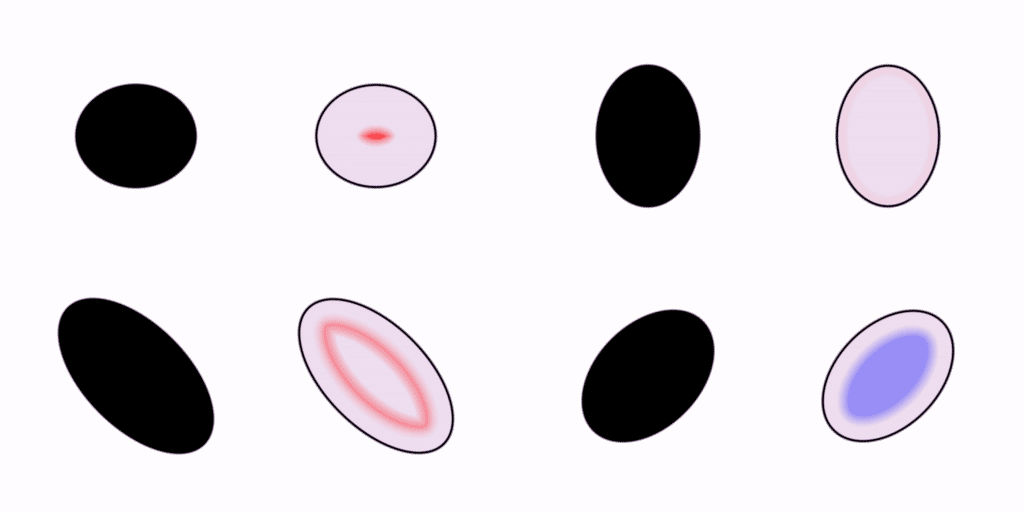
We saw earlier how the pattern of wavefronts inside a circle converges to a single focal point in the very center. In these ellipses, we can see how the focal points are kind of smeared out in comparison to the one in the circle.

I find that I can kinda squint at these examples and pick out which ones are more symmetrical or harmonious than the others from the wave patterns alone. Synesthetically, what do you think those crashing wavefronts sound like? Do some go doink while others go slap? Do the harsher-sounding ones feel less efficient?

If you were to study these patterns of wave propagation in the frequency domain, I think you would find that each shape has its own distinct spectral signature, or “vibe”.

These are the vibes from Andrés’ Vibes, Gestalts, and Realms video – a vibe being kind of like an object information packet which captures its unique qualities while remaining invariant to its location and orientation in the world simulation.

Typography is a good example of this kind of thing in practice – the letters of the alphabet have their own individual vibes, which may be slotted together into words and sentences as a gestalt. One may even bless their writing with a distinctive phenomenal character by selecting a particular font – tuning some aspects of the vibe spectrum while leaving the components important for legibility intact. One may even develop a feel for vibe tuning by playing the Kern Type online game, where you are rated for your ability to realign misaligned type.

In any case, the important thing is that shapes can have a vibe, and this vibe can be more or less symmetrical. To revisit what I wrote about harmonic resonance in my previous post:

…we can start to understand the brain as an analog, field-based computer that works to match incoming sensory information with a parsimonious interpretation. It attempts to select from an infinite set of possible interpretations of the world, and reifies the interpretation with the greatest possible symmetry. This is done in order to stabilise an efficiently interpretable model of the world from a wide array of noisy sensory inputs – and also because symmetry in such an oscillatory system is energetically efficient.

Symmetry is not necessarily important because it’s energetically efficient, but because energy efficiency is the actual operative principle which guides the system towards a solution – the problem being that of reconstructing a volumetric world simulation from a retinal image.

The inverse optics problem

Inverse problems are a class of problems which take a set of effects as input and attempt to reconstruct a set of causes as output. In the case of our subjective experience, a stable world model is continually reconstructed from the available sensory inputs.

One must assume that our auditory and somatosensory systems are continually solving inverse acoustic and inverse somatic problems, respectively – but discussion of those is beyond the scope of this post, and instead we must focus on vision. Lehar describes the inverse optics problem as follows:

The primary function of visual perception appears to be to solve the inverse optics problem, that is, to reverse the optical projection of the eye, in which information from a three-dimensional world is projected onto the two-dimensional retina. But the inverse optics problem is underconstrained, because there are an infinite number of three-dimensional configurations that can give rise to the same two-dimensional projection. How does the visual system select from this infinite range of possible percepts to produce the single perceptual interpretation observed phenomenally?

I found myself fascinated with both eyesight and photography from a young age. I spent much of my teenage years deconstructing my own sense of vision with the aid of early digital cameras and a copy of Adobe Photoshop.

One of the first novelties I discovered was how to make red-cyan anaglyphic images that could be viewed with a pair of 3D glasses. It remains miraculous to me to this day that a true sense of depth could be recreated in this manner; that all it takes is a binocular pair of images and the brain just handles the rest.

This is the inverse optics problem in a nutshell. How does the brain generate a depth map from a pair of two-dimensional images? By converging on the volumetric interpretation with the greatest symmetry.

Shock scaffolds

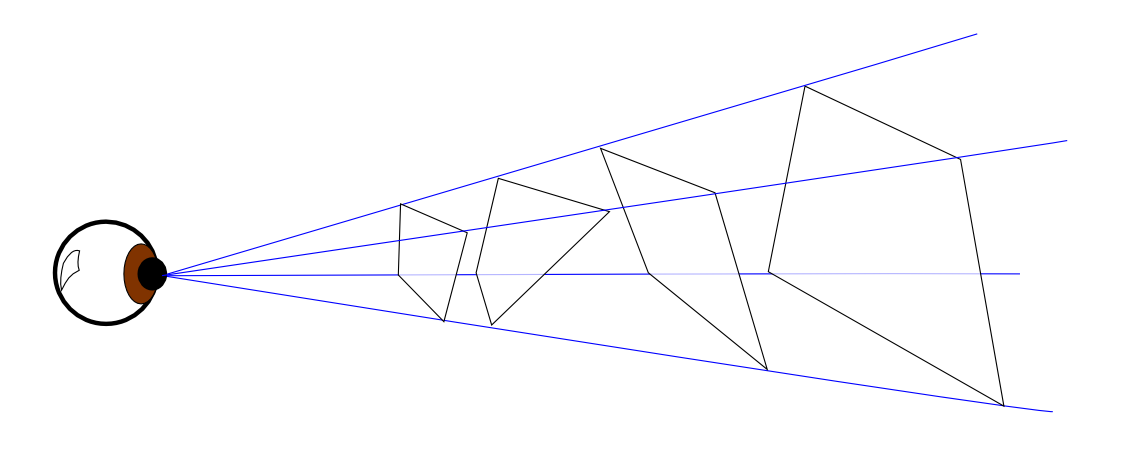
In order to explore this prospect, Lehar takes the planar flame front/grassfire metaphor and adds an additional dimension, giving us the volumetric shock scaffold:

There is a three-dimensional extension to the grassfire algorithm, known as shock scaffolds, used to compute the three-dimensional medial axis skeletons of volumetric forms such as spheres and cubes, by the same principle that the grassfire metaphor uses in two dimensions. Instead of igniting the perimeter of a two-dimensional figure, the outer surface of a volumetric form is ignited, which creates a flame front parallel to each surface, and propagating outward normal to the surface.

This allows full volumetric forms to be evaluated for symmetry. Lehar provides an illustrated description of this process, which we have animated here:

Consider a visual stimulus of a simple ellipse. By itself this stimulus tends to be perceived as an ellipse, but given a little additional context, it can also be perceived as a circle viewed in perspective. But the symmetry of the circle is entirely absent from the stimulus, so the circular symmetry must be reconstructed by reification in a volumetric spatial medium before it can be detected.

The elliptical cylinder extruded from the stimulus ellipse contains perfect plane circles embedded within it obliquely, and these circles have a perfect circular symmetry that could be detected at their center, by the perfect convergence of propagating wave fronts at those circular centers. In other words, at that special point, the circular symmetry around that point is manifest by the abrupt synchronized arrival of propagating waves from all directions simultaneously, within a disc around a tilted central axis to a focal point.

Whether the visual system uses a shock scaffold or grassfire propagation type of algorithm remains to be determined. But whatever the algorithm used in visual perception, it is one that appears to pick out the simplest volumetric interpretation in a volumetric spatial medium, from amongst an infinite range of possible interpretations, and it does so in a finite time. The shock scaffold algorithm offers one way that this kind of computation can be performed. The shock scaffold algorithm also explains why the brain would bother to do this computation in full volumetric 3D, instead of in some abstracted or compressed or symbolic spatial code, as is usually assumed. Because it is easier to pick out the volumetric regularity of an interpretation from an infinite range of possible alternative interpretations, if searched simultaneously in parallel, than it is to find that regularity where it is not explicitly present in the two-dimensional projection or other abstracted representation.

How do you see the ellipse? Is it flat against the screen, or does one of the circular interpretations burst into relief if you think about it the right way? How does it feel? Like it wants to turn itself into a circle, but the incoming stimulus of the flat screen prevents it from doing so?

We should observe that this particular stimulus is a bistable percept – it has a pair of symmetry-maximising volumetric interpretations. If you can percieve it as having depth, do you see it from above, or below? Can you flip between the two interpretations?

It is important to note how a three dimensional scene may be populated using a mixture of naïve triangulation and physical and volumetric priors. Given that we just looked at a picture of a swimming pool, you might be primed to see the circular percept from above – or perhaps if you spend a lot of time looking for flying saucers you might be more likely to see it from below. Priors can be viewed as Bayesian energy sinks in a system like this, but perhaps they could also be viewed as a form of long-term temporal symmetry?

Like an echo chamber that instantly picks out its resonant frequency from a white noise stimulus containing all frequencies, the visual system resonates to volumetric spatial interpretations that exhibit the most symmetry.

Depth maps

We’re still missing something. We have all the pieces in place to solve the inverse optics problem and generate depth maps, but what is depth, anyhow?

As Lehar points out in his Harmonic Gestalt video, there is an inverse relationship between an object’s size and the frequency of the oscillatory processes that reify it.

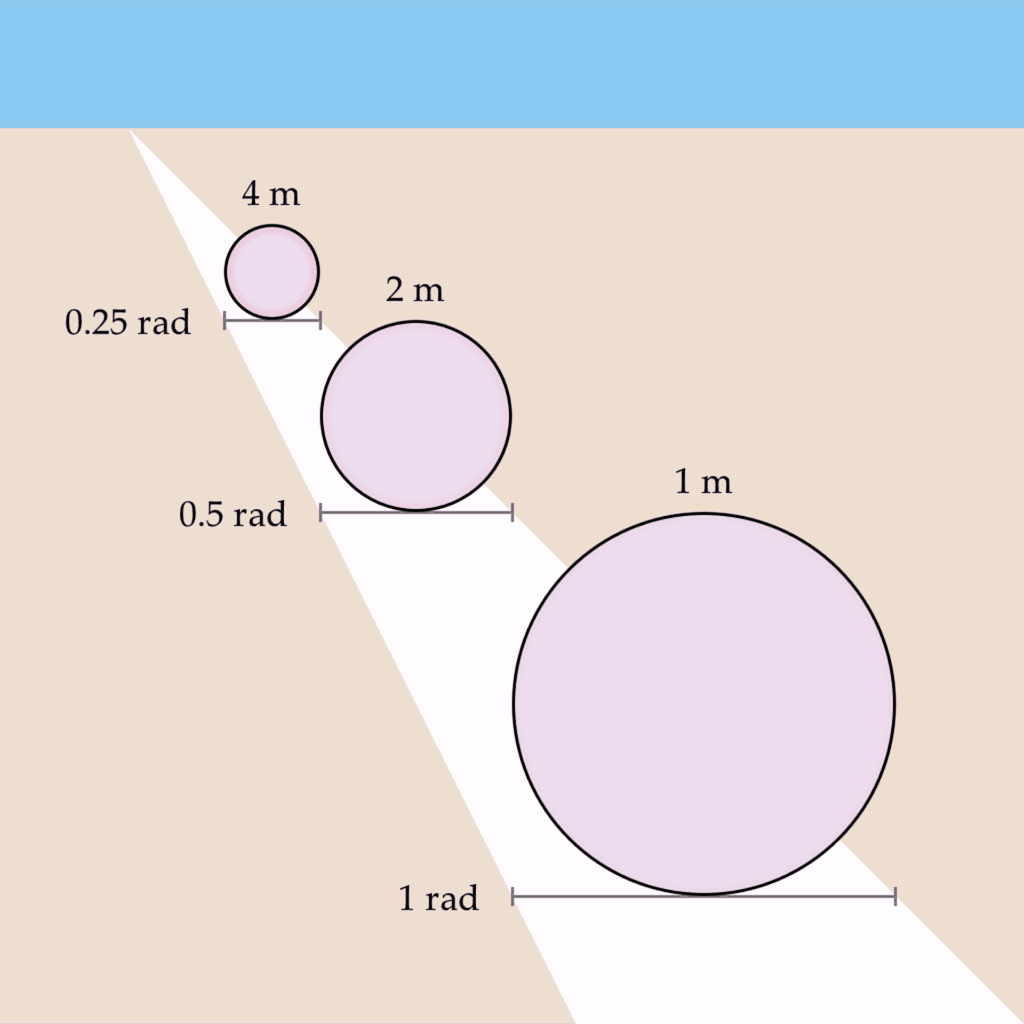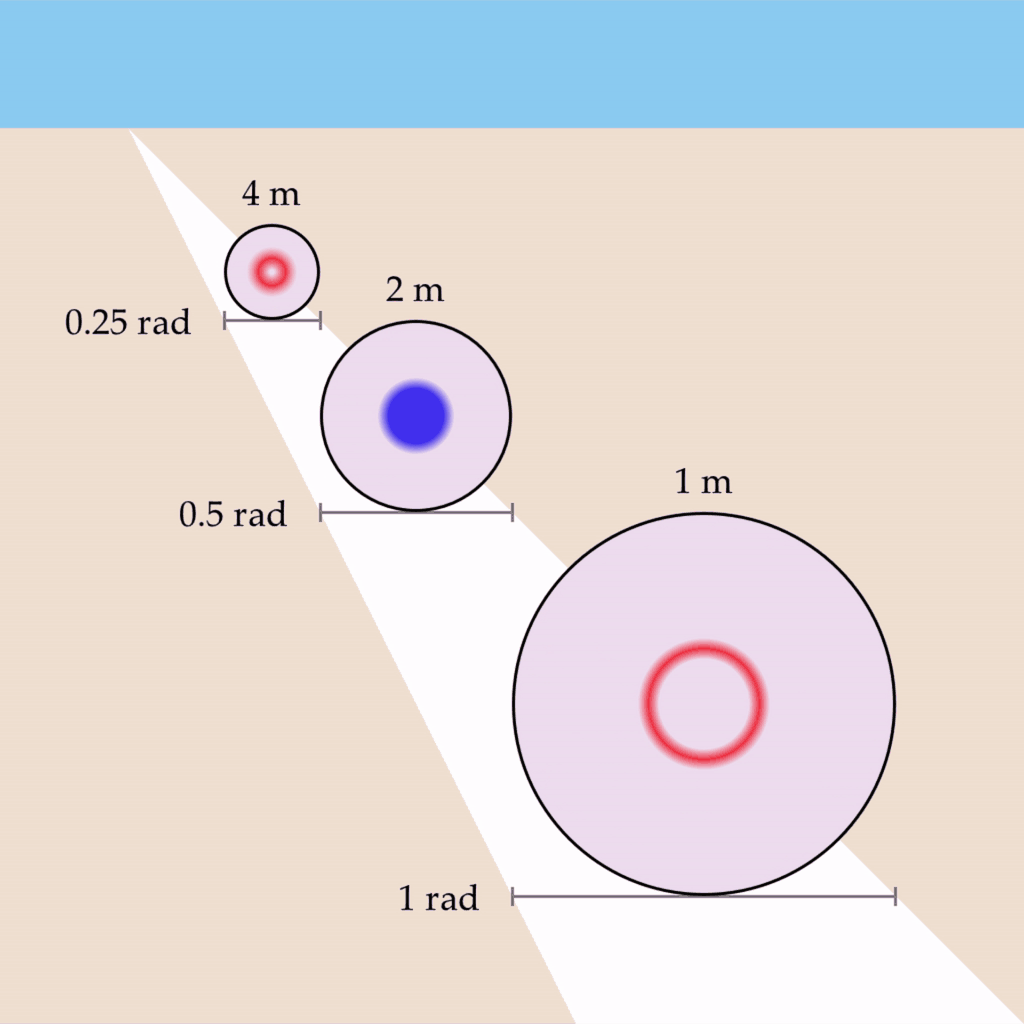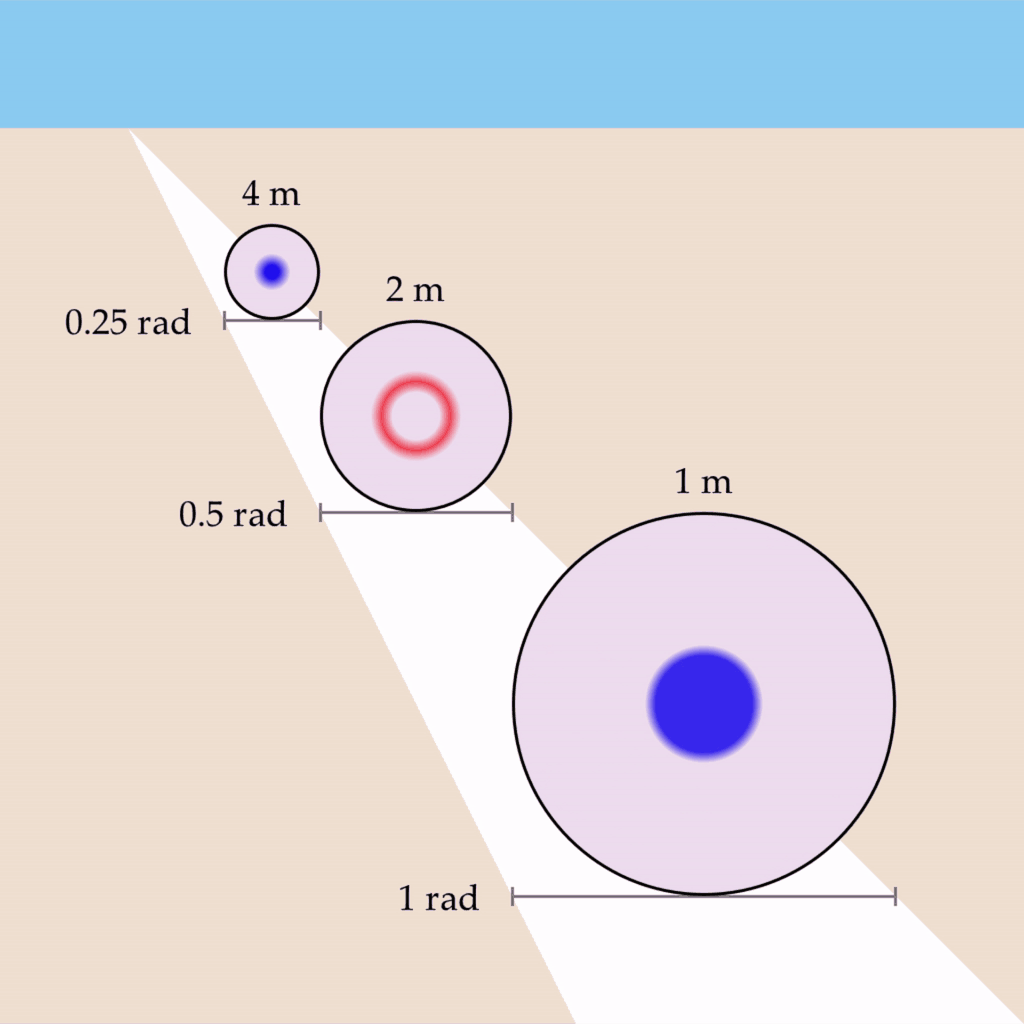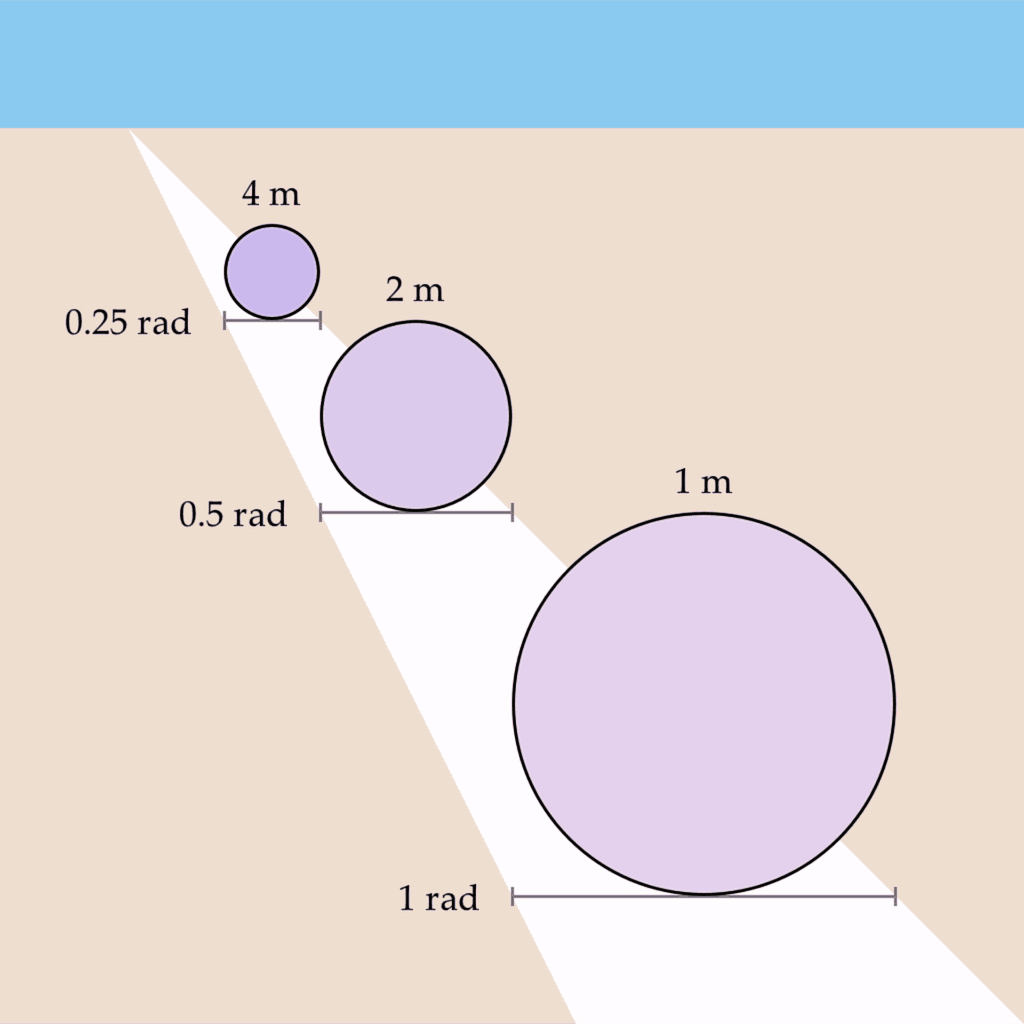
Let’s imagine that you observe three one-meter circles of the same physical size but at different distances such that they each subtend a visual angle of 0.25 rad, 0.5 rad, and 1 rad, respectively. Let’s also say that you are viewing this scene with one eye closed, and a depth map is not being created. If we take the wave propagation rate to be something like 0.5 rad/s, we would expect the circles to oscillate at 2 Hz, 1 Hz, and 0.5 Hz:

Andrés notes in Vibes, Gestalts, and Realms that a key variable may be the index of refraction. The index of refraction arises because light travels slower in certain materials than it does in a vacuum. It’s a classic piece of insight from Richard Feynman – light takes the path of least time through different media, which may not necessarily be a straight line.

From QED: The Strange Theory of Light and Matter, page 51:

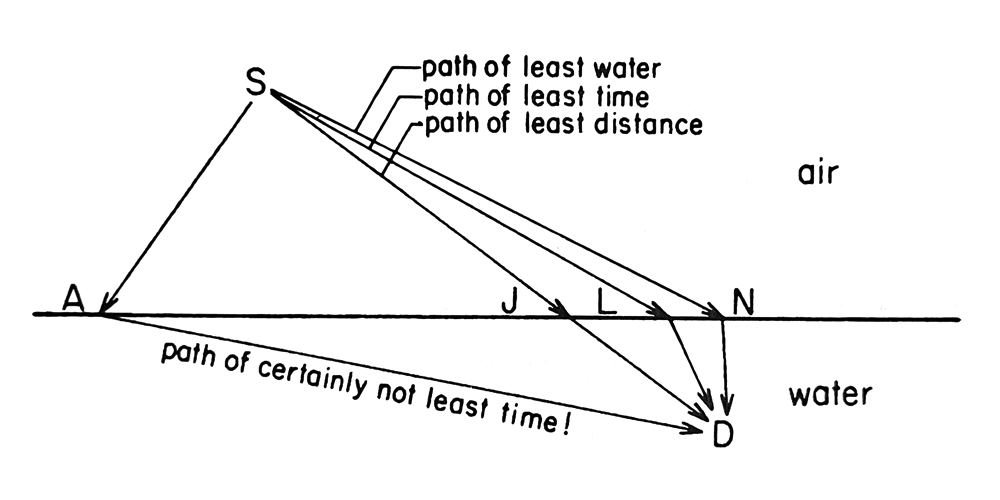
Finding the path of least time for light is like finding the path of least time for a lifeguard running and then swimming to rescue a drowning victim: the path of least distance has too much water in it; the path of least water has too much land in it; the path of least time is a compromise between the two.

Andrés expands upon this further in a more recent video, The Brain as a Non-Linear Optical Computer: Reflections on a 2-Week Jhana Meditation Retreat:

Your world simulation is being constructed with nonlinear waves bouncing off each other. So when you only have one eye, the distances between the points are going to be computed by how long it takes for a particular wave to travel from one point to another. When you integrate the two video streams, waves will also start to propagate across the z-axis. There’s a little equation there which calculates how much it’s going to travel – which corresponds to the relative displacement in the x-axis between the points in both fields.

So the depth will be a function of how far apart those two points are relative to each other in the x-axis. Waves then start to propagate as spheres, and so you have a huge collection of points that are now related with a distance function that works according to something equivalent to the generalisation of the Pythagorean theorem. The distance is not going to be √(x² + y²), it’s going to be √(x² + y² + f(z)); or f of the displacement in the z-axis. And that is the speed at which these waves propagate.

Now, there’s an interesting additional point here, which is that your worldsim is actually non-Euclidean – it’s this weird projective space, it looks like a diorama. I suspect that the way in which this depth is actually implemented involves changes to the index of refraction – to the speed at which these waves are propagating. And so the things that are further away are things where the waves propagate more slowly.

Who’s to say that the index of refraction must remain fixed in this wave medium? What if it could be changed on the fly? This is a neat idea. I’m not sure what kind of medium might support this capability, but I’d sure like to know. I discussed this with a friend, who remarked: “I’m biased against believing that any such changes are practical from an implementation perspective”. But, here we are.

Let’s say you now open your other eye, and a depth map is generated. If the depth values in the depth map were related by a reciprocal to the wave propagation rate, then perhaps the shapes could all vibe at the same fundamental frequency?

For example, if the wave propagation rate for the region bounding each circle was changed to be 0.25 rad/s, 0.5 rad/s, and 1 rad/s, respectively, then the circles would oscillate at a uniform rate of 1 Hz:

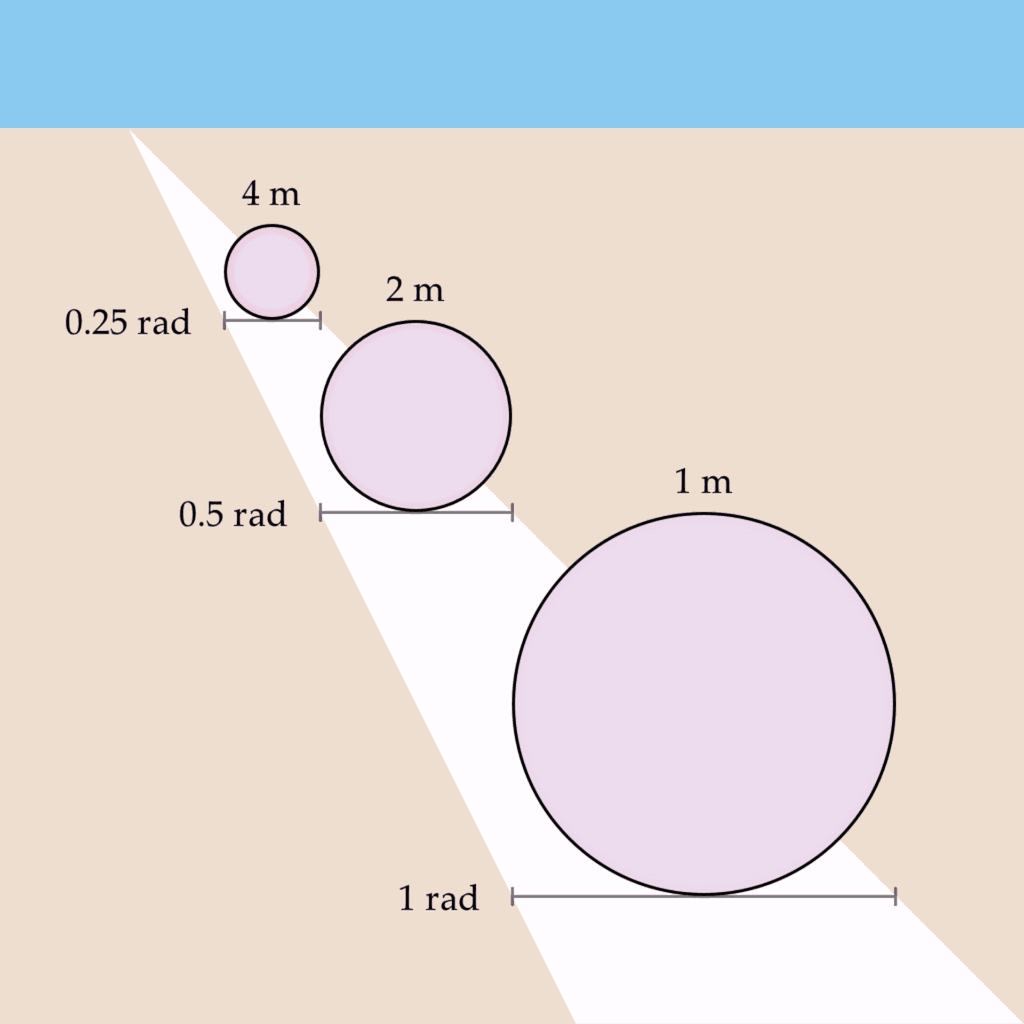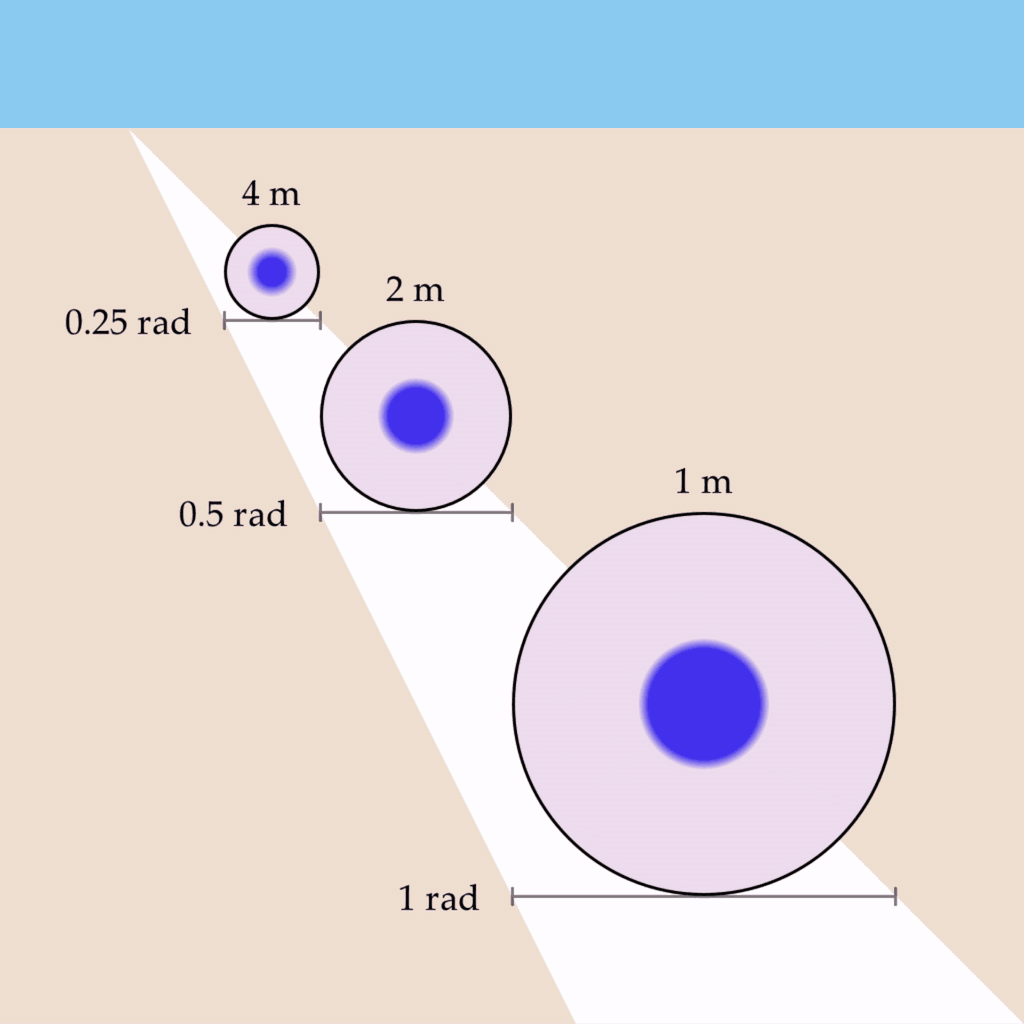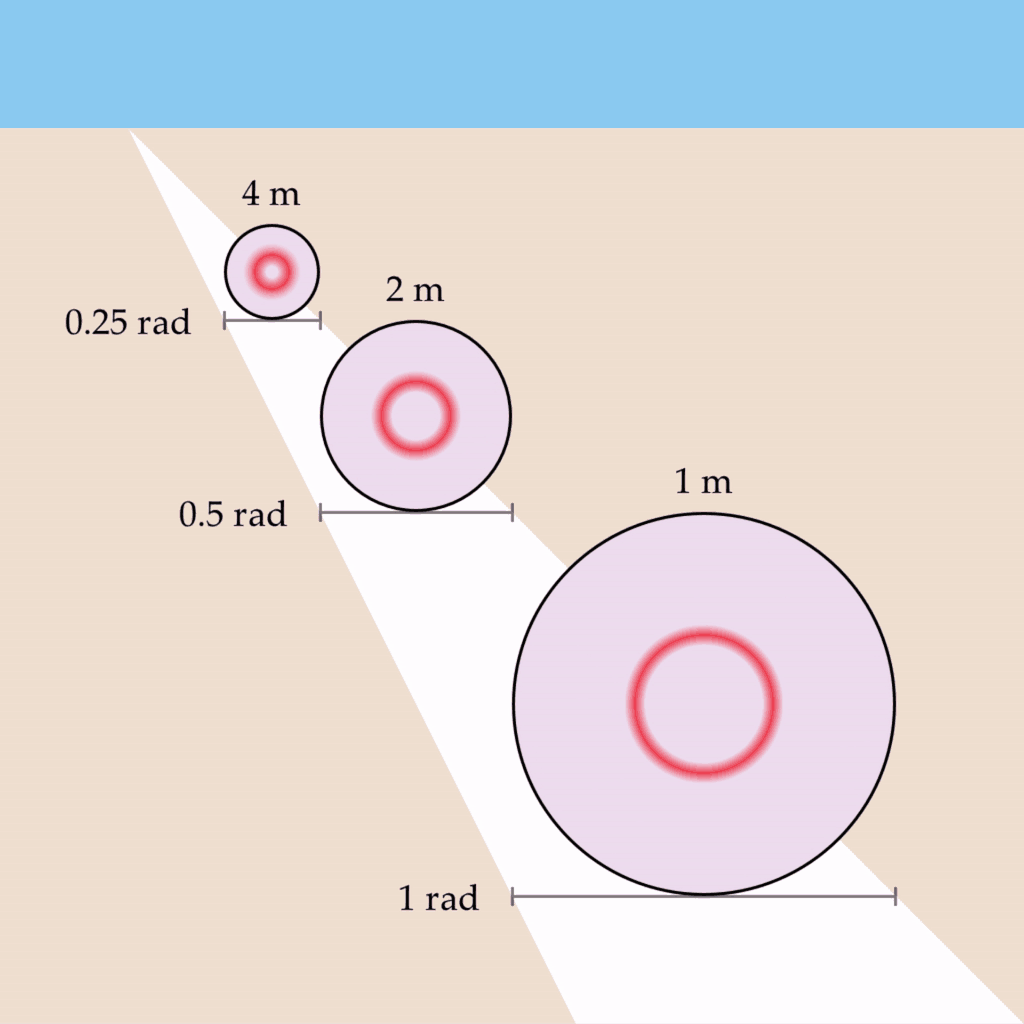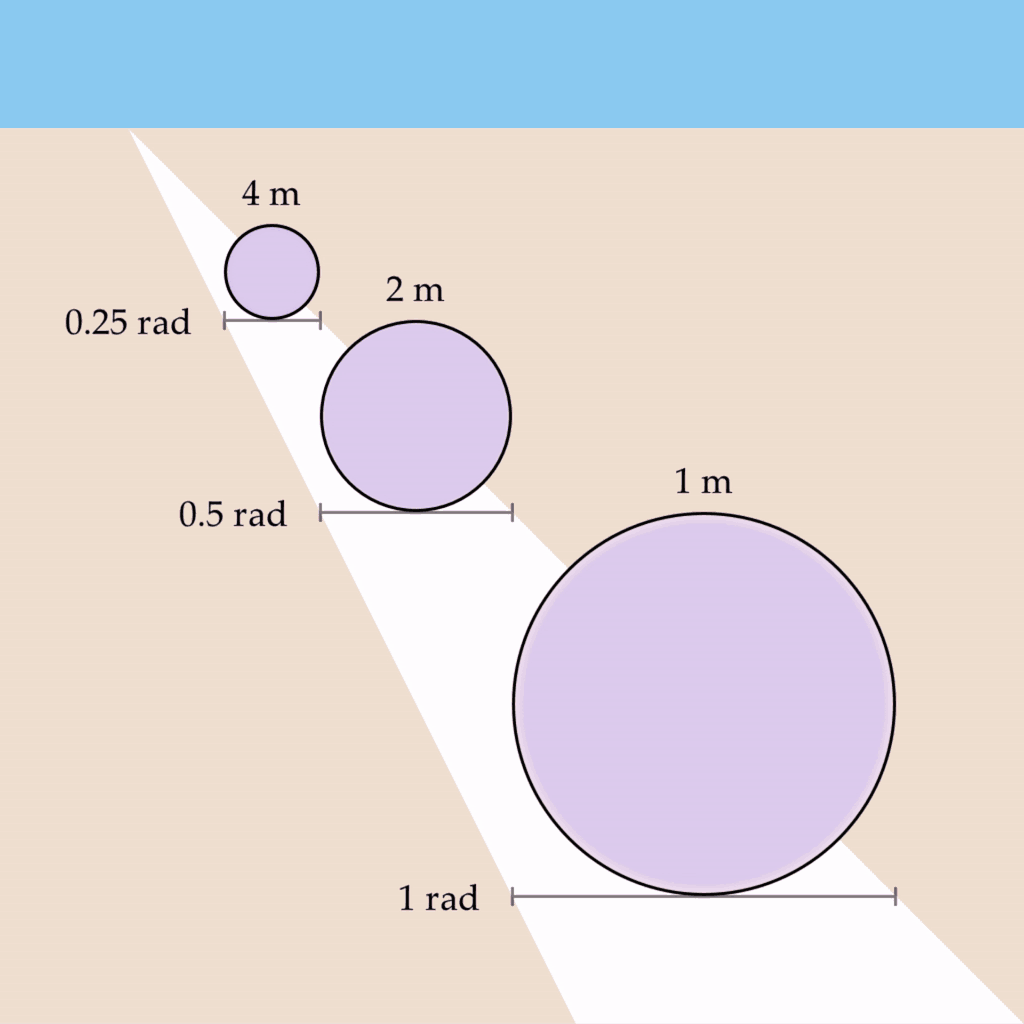
This phenomenon has several desirable properties – it preserves the shape’s vibe invariant of depth, as well as implementing the conformal mapping required for the phenomenon of phenomenal perspective.

This feels like a sufficiently satisfying insight with which to wrap up our tour. Depth perception can be a visceral, ineffable experience, but here we see its inherent emptiness laid out: depth is just variation in wave propagation rate.

Epistemics

So here we have it – a model for a field-based computing process that solves the inverse optics problem by maximising the energy efficiency of its generated world model.

It’s a pretty strange kind of computer! It’s so alien that it almost feels like it’s not a computer at all, at least in any traditional sense. Hey, maybe real aliens would be so advanced that their computers would work something like this. After all, evolution has had millions of years to perfect its designs, while the history of computer science is measured in mere decades.

Near the end of his paper, Lehar includes some discussion about how he regards his model:

The theory of vision presented herein may seem somewhat vague and ill-specified as a computational model of perception. That is why the theory is presented not as a model of visual perception by phase conjugation, nor even by a forward-and-reverse grassfire or shock scaffold algorithm, because there is neither sufficient evidence for those exact algorithms in perception, nor are those algorithms sufficiently specified to be a perceptual model in the usual sense. Instead, the primary message of this paper is more general, and it comes at several levels with various degrees of certainty at each level.

First and foremost, the message of this paper is that visual perception has a constructive, or generative function that constructs a complete virtual world of experience based on a relatively impoverished sensory input. The information content of that world of experience is equal to the information content of a painted model world, like a diorama, or a theater set, with volumetric objects bounded by colored surfaces embedded in a spatial void.

In other words, the representational strategy used by the brain is an analogical one. That is, objects and surfaces in the world are represented in the brain not by an abstract symbolic code, as suggested in the propositional paradigm of Artificial Intelligence, nor are they encoded by the activation of individual cells, or groups of cells representing particular features in the scene, as suggested in the neural network or feature detection paradigm. Instead, objects are represented in the brain by constructing full spatial effigies of them that appear to us for all the world like the objects themselves – or at least so it seems to us only because we have never seen those objects in their raw form, but only through our perceptual representations of them.

Andrés recently posted an excerpt on his blog from The Maxwellians by Bruce J. Hunt. This is a book that tells the story of the group of people who developed and popularised James Clerk Maxwell’s theory of electromagnetism.

I wound up reading it myself. I became somewhat enamoured with the intuitive mechanical models that the Maxwellians developed in order to understand and communicate their theories prior to settling on the field theory we use today – Maxwell’s vortex and idle wheels, Lodge’s beaded strings and pulleys, and FitzGerald’s wheel and band model, to name a few of these speculative contraptions.

From The Maxwellians, page 76:

These illustrative models were meant to be instructive, not explanatory. They added nothing essentially new to the theoretical account of a phenomenon but simply made it more vivid. They were certainly not meant to be realistic: Maxwell did not think electromagnetic induction was traceable to the turning of cranks and the meshing of gears, nor did Heaviside and Lodge think dielectric polarization was really a matter of movable pistons or of strings and buttons. As FitzGerald put it, illustrative models were intended as analogies of phenomena, not likenesses; they offered a similitude of relations, not of things.

I was curious if any physical manifestations of these models remained in existence, so I emailed Bruce J. Hunt to ask. There were none left, but he kindly linked me to a document on his website which contained a number of illustrations.

From Lines of Force, Swirls of Ether, page 4:

FitzGerald’s wheel-and-band ether model (unstrained). Source: diagram by the author. FitzGerald’s 1885 model pictured the electromagnetic ether as an array of wheels set on vertical axles and connected to their neighbours by rubber bands running around their rims. The spinning of the wheels represented a magnetic field, while the stretching or loosening of the bands that resulted from unequal rotation of the wheels represented an electric field. The model is shown here in its unstrained state, with the wheels either stationary or all spinning at the same rate. The bands are thus neither stretched nor loosened, and the model represents a region in which there is no electric field and the magnetic field is either zero or constant.

I’d say it’s the case that Lehar’s flame fronts and shock scaffolds occupy a similar status – intuitive, mechanical models that precede a more general theory, be that non-linear wave computing or something much like it.

The initial first pass of a flame front visualisation is a tremendous visual aid for gauging the inherent symmetries in a given shape. However, there’s aspects of the flame front metaphor that feel off with regards to my own intuition – we certainly don’t see these waves bouncing around when we open our eyes. Perhaps the medium behaves in a way that is more immediate, more elastic, performing reification via something more like electromagnetic interpolation? Or perhaps these oscillatory processes happen are performed in some kind of hidden layer, situated adjacent to our phenomenal fields?

All of this deserves investigation, and indeed Lehar closes off with such a call to action:

Whether perception employs anything like a reverse grassfire or shock scaffold or phase conjugate type algorithm, the effect of visual processing clearly exhibits properties as if perception were using some kind of reverse shock scaffold type principle in perceptual reification, in which central symmetries that are detected in the stimulus are interpolated and/or extrapolated back out again to produce an explicit volumetric structure in experience with both modal and amodal components, as the simplest, most geometrically regular structural interpretation of configuration in the world that is most likely to have been the cause of the given visual stimulus. This computational process is real, and demands a neurophysiological explanation.

Do we need a perfectly-specified theory in order to search for its neural correlates? This is where I’d like to revisit connectome-specific harmonic wave theory. Selen Atasoy’s team found that the 4^th and 8^th functional harmonics mapped onto the retinotopy of the visual cortex:

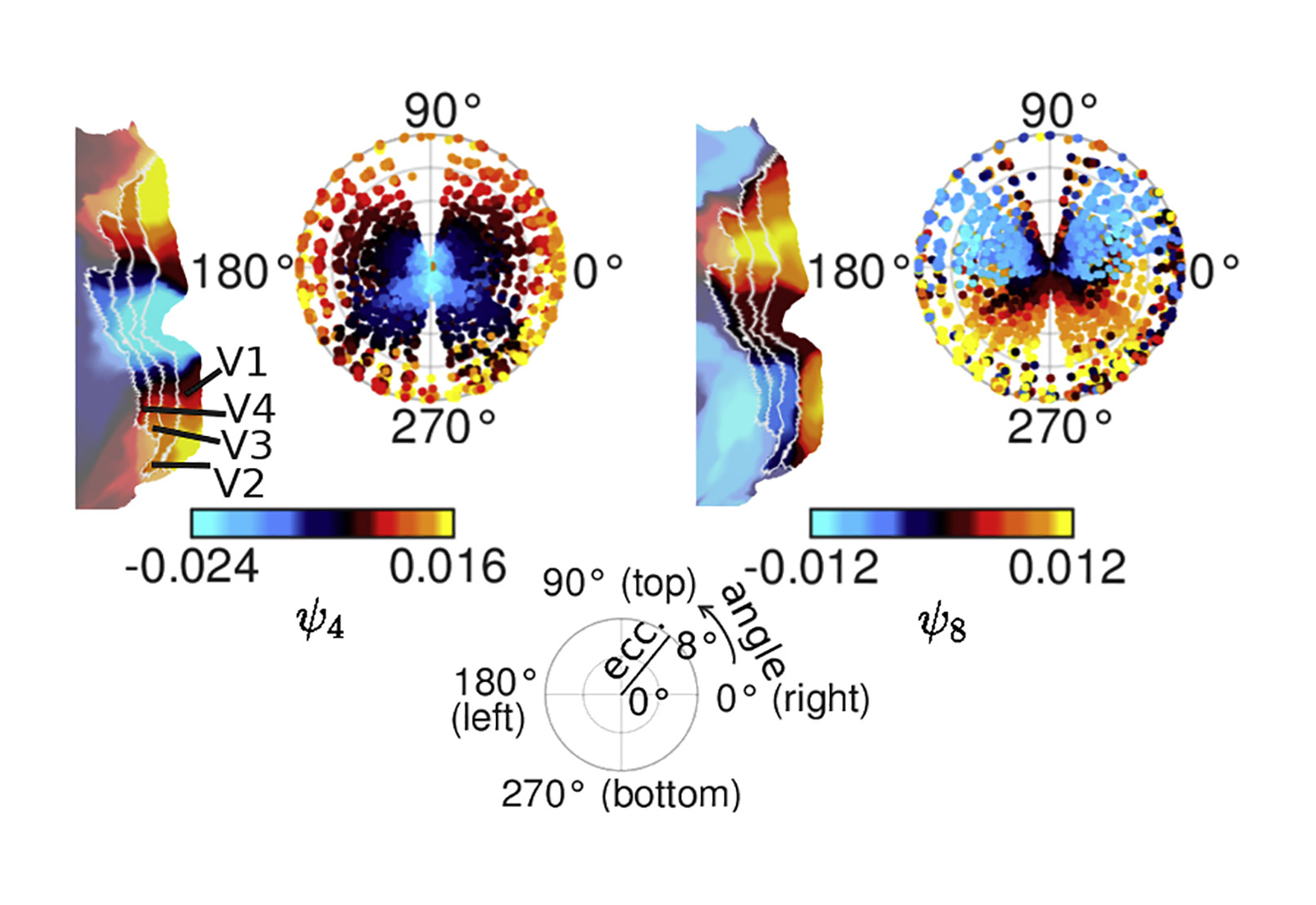
Retinotopies of functional harmonics 4 and 8. Each panel shows, on the right, the colors of the respective functional harmonic in early visual areas V1–V4 on a polar plot of eccentricity (distance in degree from the fovea) and angle on the visual field (see legend at the bottom of the figure). On the left, the respective functional harmonic is shown on a flat map of early visual cortex (left hemisphere). V1, V2, V3, and V4: visual areas 1, 2, 3, and 4.

I wonder if we could detect pertubations in these functional harmonics in accordance with harmonic resonance theory? It could be as simple as putting someone in a virtual reality headset and showing the subject geometric figures of various shapes and sizes. Would something spiky generate strong enough vibes to show up on EEG or fMRI?

Neuralink trials are also currently underway. When their most recent show and tell video was published I stayed up until two in the morning watching it. Visual neuroscientist Daniel L. Adams is working on restoring sight for the blind, and presented an inspiring demonstration of a macaque monkey responding to phosphenes injected by a visual cortex implant. What might the phenomenology of those tell us about non-linear wave computing? Are they regular in shape? Might they have rainbow fringes?

But we cannot know yet, because the monkey cannot tell us. Yet.