Path integrals and orbifolds: What is it like to be a cube?
Posted on 1 June 2025 by
One of the core philosophical questions which any theory of consciousness worth its salt must answer is, what is it like to be something? Or, put differently, how do physical states map onto qualia states? This is what Mike Johnson calls the reality mapping problem.
One of the few people I know of who have proposed concrete claims to this end is Andrés Gómez Emilsson of the Qualia Research Institute. Andrés is a proponent of electromagnetic field theories of consciousness, and has a curious answer to the reality mapping problem involving path integrals. I attempted to summarise his stance in a previous post:
- The physical state which corresponds to subjective experience is the electromagnetic radiation trapped within a topologically closed region of the electromagnetic field – for example, a closed surface where the magnetic flux density is zero – somewhere within the brain.
- The electromagnetic radiation explores all possible paths through the enclosure in parallel, and the superposition of all these paths – the path integral from quantum electrodynamics – forms the wave patterns which we perceive as the phenomenal fields. This is where the computation happens.
- Variation in permittivity of the substrate underlying the topological pocket adjusts the speed of the radiation passing through the substrate, shaping the path integral as is computationally useful.
Even without making any assumptions with regards to what substrate we think consciousness is implemented upon – path integrals are quite a rich mathematical object, and I think they seem like a compelling place to start exploring.
What are path integrals?
The path integral as a mathematical construct comes from Richard Feynman’s path integral formulation of quantum mechanics. It states that rather than following a single trajectory like a classical object, a quantum particle’s behavior emerges from the superposition of every conceivable path it could take. Each path contributes a quantum phase which depends upon how long or indirect it is. In most cases, these phases interfere destructively, cancelling each other out at the destination – typically leaving only those paths which are close to the classical trajectory.
This is necessary in order to explain things like the interference patterns left by light passing through a diffraction grating, or how light is observed to take the path of least time through a variable refractive index or variable permittivity medium. From QED: The Strange Theory of Light and Matter, page 51:
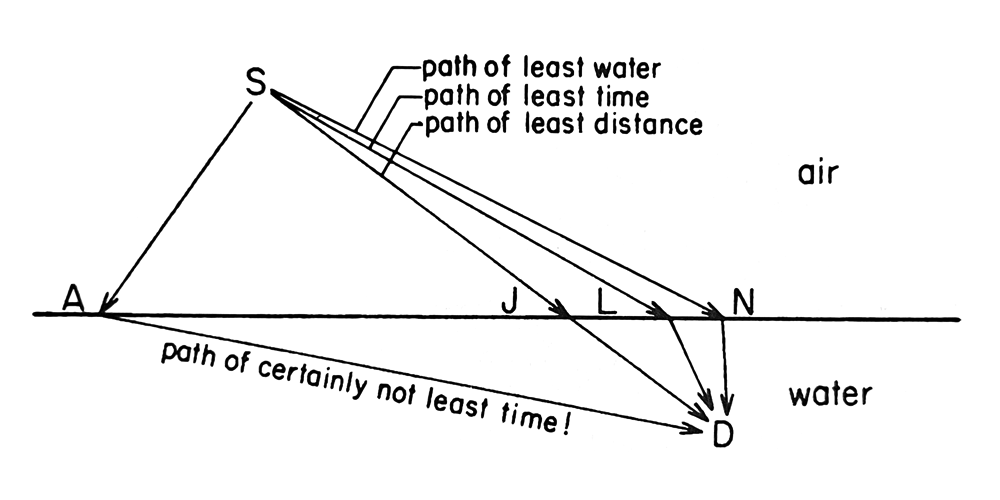
Finding the path of least time for light is like finding the path of least time for a lifeguard running and then swimming to rescue a drowning victim: the path of least distance has too much water in it; the path of least water has too much land in it; the path of least time is a compromise between the two.
For a comprehensive exploration of the mathematics underlying path integrals, I recommend the Physics Explained video, How Can Light Travel Everywhere at Once? Feynman’s Path Integral Explained:
We notice something interesting when we compare ten paths which curve a lot between A and B, and ten paths that are close to straight lines between A and B. We see that the final arrows for the curvy paths tend to point in different directions, and the arrows for the near straight paths tend to point in similar directions, and thus the final contribution of the straight line paths to the overall probability is much more significant than the curvy paths.
Even without being explicitly stated, path integrals would be implicit within Andrés’ ontology, as presumably any electromagnetic radiation trapped within neural structures would also explore all possible paths within those structures. His claim is that the resulting interference pattern is one and the same with the phenomenological content of subjective experience – i.e., qualia.
What is it like to be a path integral?
This might be difficult to wrap your head around without any concrete examples. In Andrés’ video, Creating the Screen of Consciousness: Cavity Grids, Beam Splitters, and Path Integrals, he asks the viewer to imagine what it’s like to be light inside differently shaped electromagnetic cavities with total internal reflection, using a cube as an example:
Now imagine – if what it’s like to be the light in that system is the superposition of all possible paths – when you’re in one of these compartments, and it’s perfectly mirrored, what would happen is that all the paths would start to look the same. The standing wave pattern – the main mode within that compartment – is symmetrical. Rotationally symmetrical in the case of a sphere, or if it’s a hexagon it could be symmetrical in other ways, you’d have reflection and rotation in six ways – and so all of those perspectives cancel out and merge with each other.
Let me give you a quick example, here. One of the classic thoughts that I have is – what is it like to be a cube, from the point of view of this path integral perspective? Well – it’s like the superposition of what it’s like to be here, plus what it’s like to be here, and what it’s like to be here, and so on. And in practice, it would be something like this – it would be like this strange thing where there’s actually just one corner. Right? Because the cube looks the same from each of those corners. So, there’s many perspectives from within the object where the object looks the same to itself – and all of those collapse into the same perspective.
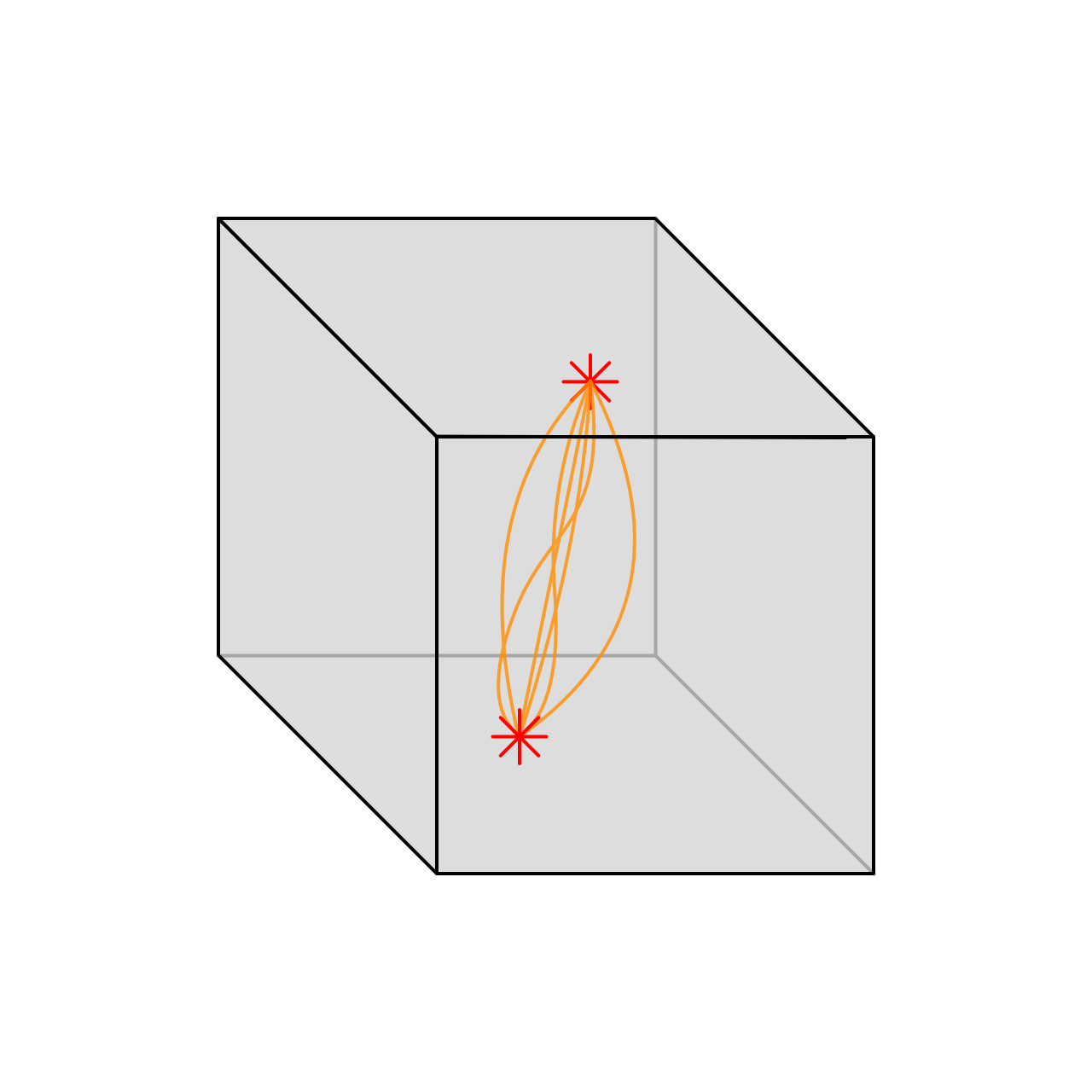
I have one thing to add to this, which is that if we take this as given, and if we count all the symmetries – what it’s like to be a cube is not what it’s like to be one corner of a cube, but instead it’s what it’s like to be a sixth of a corner of a cube, given that the corner itself has its own three-way mirror symmetry:
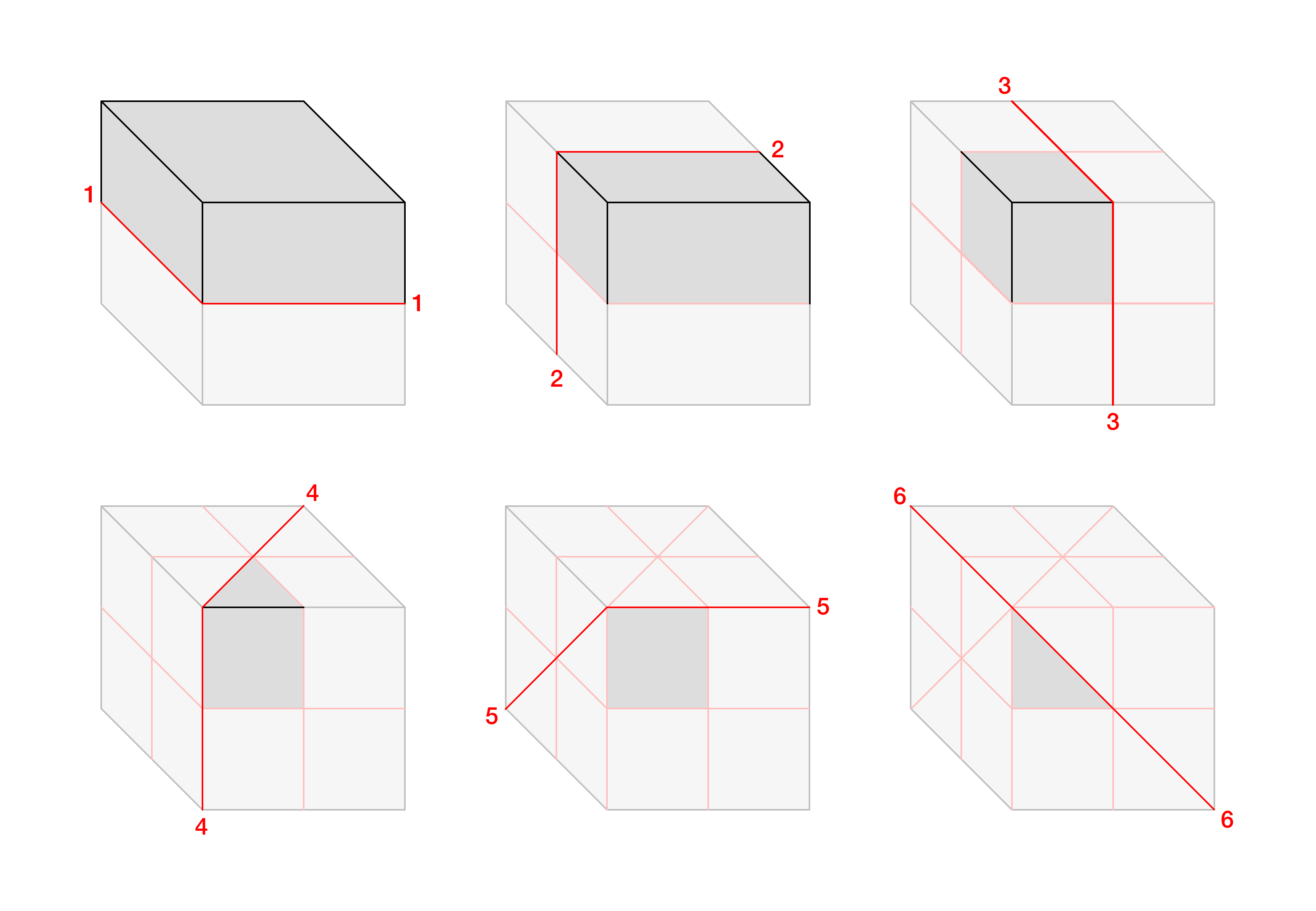
The quotient space which encodes how each point maps to its images is known as the orbifold. In the case of our cube, in John Conway’s notation the orbifold in question is identified as the ∗432 spherical symmetry group. From The Orbifold Notation for Two-Dimensional Groups (Conway and Huson, 2002):
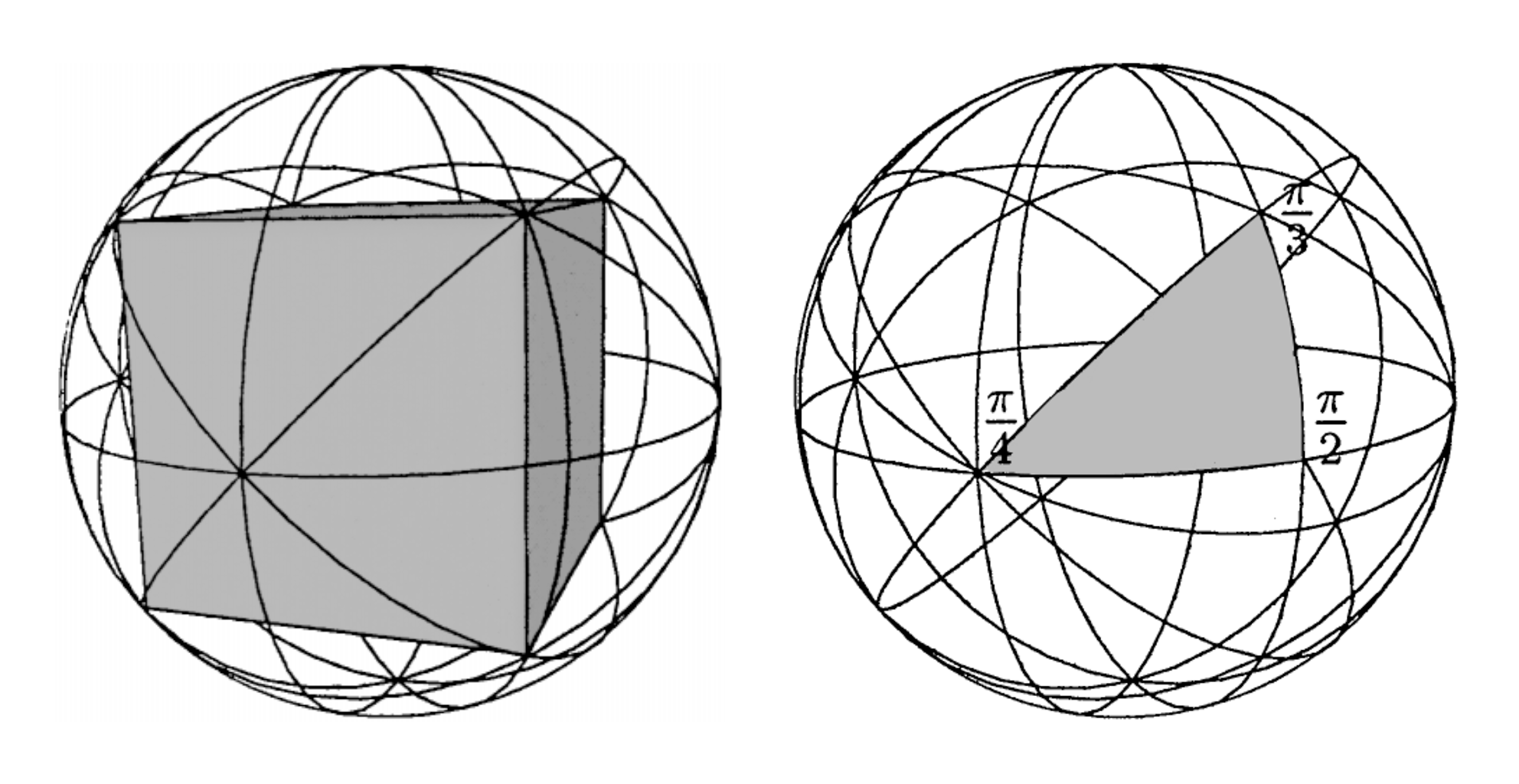
∗432 associated with the symmetry group of the cube.
An orbifold is a fairly abstract mathematical object used to encode the symmetries in an object – imagine a kaleidoscope, where you only need to understand one small wedge to know the whole pattern. In Conway’s orbifold notation, two dimensional orbifolds are composed from six primitive features – the four most common are wonders (○), gyrations (N), kaleidoscopes (*N) and miracles (×), which encode translations, rotations, reflections, and glide reflections, respectively. Represented visually, they resemble a piece of paper cut up and rejoined to itself. From Unification and classification of two-dimensional crystalline patterns using orbifolds (Hyde et al., 2014):
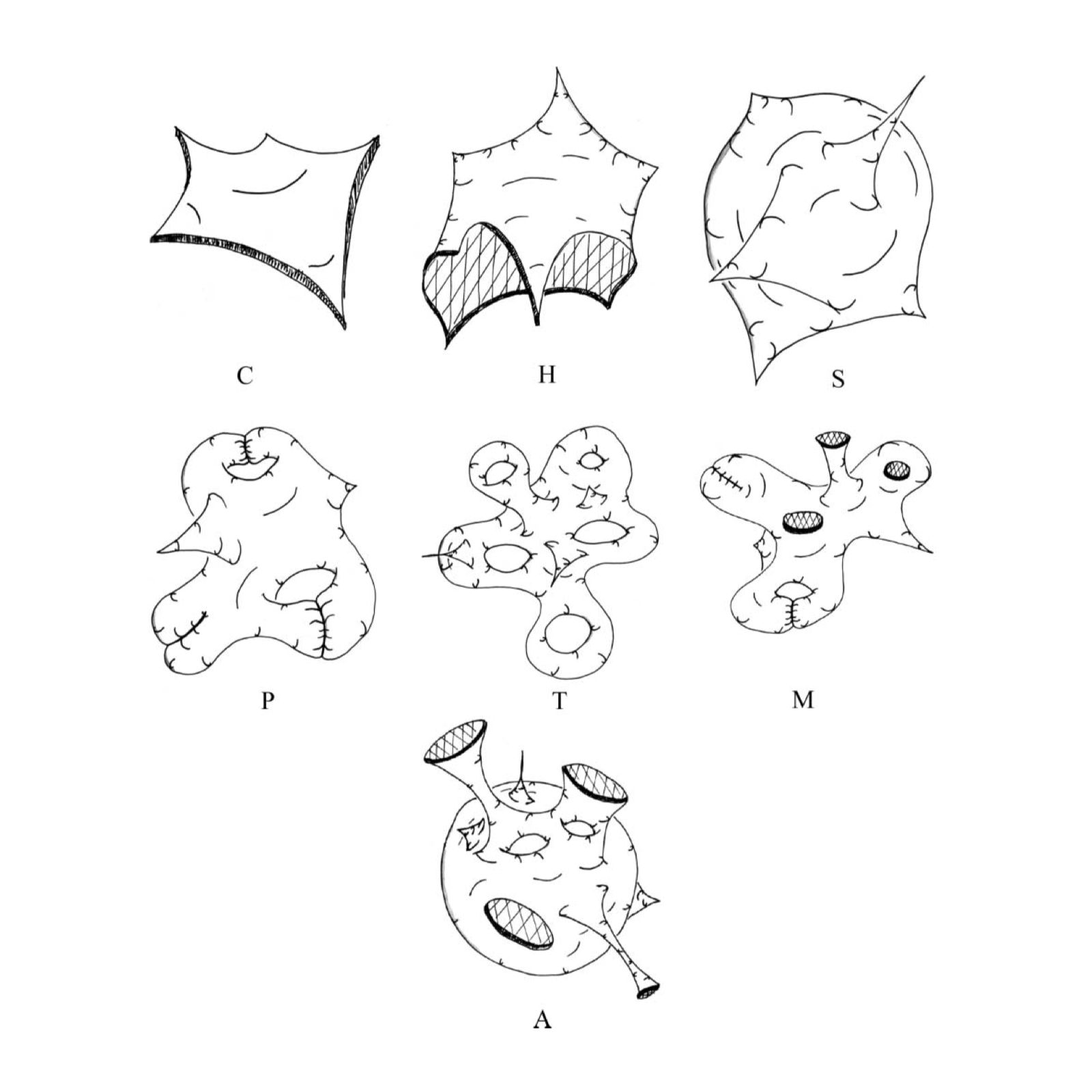
The naked orbifold ∗432 captures the cube’s geometry, but not its contents. If its faces were painted with particular colours, or if its volume was filled with some substance – like a variable density gas, or an electromagnetic field – those scalar or vector values do not live on the orbifold unless we decorate it with a section of the appropriate orbifold bundle. So perhaps, what it’s like to be a cube is what it’s like to be a field-decorated orbifold ∗432.
However, this statement only holds if the contents of the cube also respect the ∗432 symmetry group. For instance, if we painted our cube in a particular way, this could change the specific symmetry group we need. An example can be found in the book, The Symmetries of Things (Conway et al., 2008), page 60:

432; an unmarked cube has type *432.
In the case of an electromagnetic cavity, there’s two things we can change in order to make or break its symmetries – we can change the amplitudes and phases of the radiation it contains, or we can change the shape of the cavity itself.
In a closed cavity, any paths in the path integral must loop back on themselves – and only certain paths will constructively interfere and contribute to the final wave function amplitude. The frequency of the radiation determines how much phase accumulates along each path, and only those closed loops whose total phase is a multiple of 2π will survive the destructive interference. The resulting interference patterns correspond exactly to the cavity’s resonant eigenmodes, naturally leading to the quantized resonant modes we observe:
It’s easy to see how some combinations of modes preserve various spatiotemporal translation, rotation, and mirror symmetries, while others do not – and this is down to the spectrum of radiation within the box. These different modes would presumably generate quite differently-shaped experiences.
Of course, it’s also possible to more directly change the shape of the experience by changing the resonator’s boundary conditions. It’s possible to simulate how radiation propagates inside quite complicated shapes – and Bijan Fakhri explored this in his writeup, The Electrostatic Brain: How a Web of Neurons Generates the World-Simulation that is You:
What is it like to be you?
The ultimate claim here is that this is how our subjective experience – our world simulation – is built. Start with a sphere or a torus or something and progressively break a few symmetries, until you have something that looks like your inner world. All that you are, all the structure and texture of the somatic and visual fields – just electromagnetic radiation in a you-shaped resonant cavity:

Open questions
I don’t think this is a complete picture – I still don’t understand what colour might be, for instance. That said, I expect this model should work well when considering geometric qualia like shape and space. Anyway, aside from the issue with colour, I have a couple of other questions I’d like to find answers for:
How do path integrals relate to valence?
In Mike Johnson’s Principia Qualia, he proposes that:
Given a mathematical object isomorphic to the qualia of a system, the mathematical property which corresponds to how pleasant it is to be that system is that object’s symmetry.
If the mathematical object in question so happens to be this path integral – or at least, the corresponding wave function – how do we calculate its symmetries, and will this map appropriately to how we experience valence?
What would this imply about reality? Does electromagnetic radiation want to inhabit states corresponding to symmetric path integrals – and if so, why?
What should be the epistemic basis for the path integral theory?
How can we ground all this empirically? We’d need to run some quite invasive tests in order to verify any electromagnetic field theory of consciousness – if that is even possible. However, while remaining agnostic with regards to a specific substrate, I think there’s a reasonable phenomenological basis for the idea that subjective experience corresponds to some kind of wave mechanics in a closed cavity.
Nitrous oxide is an easily accessible substance which reliably stimulates my somatic field in a way highly reminiscent of Bijan’s simulations, and I could probably list a wide variety of more or less accessible phenomena which also make sense under a wave mechanics model of subjective experience – including meditative cessation states and psychedelic ringing artifacts. Constructing questionnaires or psychophysics experiments in order to collect more rigorous evidence for this claim is left as an exercise for the reader.
On the other hand, Andrés’ claims about merged perspectives in geometrically symmetric states are on somewhat more difficult ground. He has a number of anecdotes about strange experiences which make sense if you view them as what happens when you remove most of the asymmetries from experience – but they generally involve more extreme or idiosyncratic psychedelic states. As he explains:
The reason why I even started to think about this in this way, is that on high dose psychedelics you have this very strange property where you might be experiencing this very complex intricate fractal with lots of mirror reflections – and then you look at it from a certain internal perspective and then the whole thing collapses into just one point.
Meaning that our type of consciousness is not just like a painting, where the distance between two images is measured by how many pixels you need to flip to go from one image to the other – because here we have a case where a super complex fractal is right next to a point – so it’s much more along the lines of the configuration space of two mirrors that are parallel to each other. Like, if you’re slightly off – you will see lots of reflections but you will still have a shape, you’ll have this trumpet-like, tunnel-like shape which becomes parabolic and divergent. But the moment you get it perfectly aligned – then the whole thing collapses, and it feels like an infinite space without any distortions.
At my end, I’ve had several highly symmetrical, topologically disorienting experiences while on DMT which also point in this direction, but I’m really not sure how to recreate them in a repeatable manner – let alone construct the kind of study which would convince the more skeptical reader. Creative ideas are welcome.
